Dependent Types
From theory to practice
D. Plaindoux | ScalaIO 2024
Why Dependent Types?
- Reinforcing programme security
- Critical software
Dependent Types and Blockchains
- Tezos with Coq, Cardano with Agda
- Tezos byte code (Michelson) with MI-CHO-COQ
- Proof of laws e.g. consensus
Understanding Dependent Types means
- Learn from foundations
- Focus on a core calculus
- Design a language!
A short definition
A dependent type is a type whose
definition depends on a value
Dependencies everywhere!
- terms depend on terms aka λ→
- terms depend on types aka λ2
- types depend on types aka λω
- types depend on terms aka λP
All combinations with λC or Calculus of Constructions
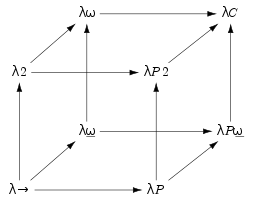
The lambda cube
☕️ Break
☕️ Break
P0 ... Pn when premisses P0 ... Pn are verified
--------- then
C we conclude C
☕️ Break
P0 ... Pn when premisses P0 ... Pn are verified
--------- then
C we conclude C
Γ type bindings i.e. hypothesis
☕️ Break
P0 ... Pn when premisses P0 ... Pn are verified
--------- then
C we conclude C
Γ type bindings (X : T) i.e. hypothesis
Γ ⊢ A : T Given Γ, the term A inhabits the type T
Language λ1
x ∈ Variables
i ∈ Identifiers
Language λ1
x ∈ Variables
i ∈ Identifiers
e ::=
λ(x).e -- Abstraction
e e -- Application
x -- Variable
Language λ1
x ∈ Variables
i ∈ Identifiers
e ::=
λ(x).e -- Abstraction
e e -- Application
x -- Variable
t ::=
i -- Basic types
t → t -- Function type
Functions
λ-expressions: abstraction and application
Functional type | M → N
Γ, x : M ⊢ b : N
-------------------
Γ ⊢ λ(x).b : M → N
Functional type | M → N
Γ, x : M ⊢ b : N
-------------------
Γ ⊢ λ(x).b : M → N
Γ ⊢ f : M → N Γ ⊢ e : M
--------------------------
Γ ⊢ f e : N
λ2 : λ1 and dependent functional type
x ∈ Variables
i ∈ Identifiers
e ::=
λ(x).e -- Abstraction
e e -- Application
x -- Variables
t ::=
i -- Basic types (int, ...)
t → t -- Function type
λ2 : λ1 and dependent functional type
x ∈ Variables
i ∈ Identifiers
e ::=
λ(x).e -- Abstraction
e e -- Application
x -- Variables
i -- Basic types (int, ...)
e → e -- Function type
λ2 : λ1 and dependent functional type
x ∈ Variables
i ∈ Identifiers
e ::=
λ(x).e -- Abstraction
e e -- Application
x -- Variables
i -- Basic types (int, ...)
e → e -- Function type
Π(x:e).e -- Dependent functional type
type -- type of type
λ2 : λ1 and dependent functional type
x ∈ Variables
i ∈ Identifiers
e ::=
λ(x).e -- Abstraction
e e -- Application
x -- Variables
i -- Basic types (int, ...)
e → e -- ≡ Π(_:e).e
Π(x:e).e -- Dependent functional type
type -- type of type
Dependent functional type | Π(x:M).N
type of return value varies with its argument
Γ, x : M ⊢ b : N
--------------------------------
Γ ⊢ λ(x).b : M → N
Γ ⊢ f : M → N Γ ⊢ e : M
--------------------------
Γ ⊢ f e : N
Dependent functional type | Π(x:M).N
type of return value varies with its argument
Γ, x : M ⊢ b : N
--------------------------------
Γ ⊢ λ(x).b : Π(_:M).N
Γ ⊢ f : Π(_:M).N Γ ⊢ e : M
-----------------------------
Γ ⊢ f e : N
Dependent functional type | Π(x:M).N
type of return value varies with its argument
Γ, x : M ⊢ b : N
--------------------------------
Γ ⊢ λ(x).b : Π(x:M).N
Γ ⊢ f : Π(_:M).N Γ ⊢ e : M
-----------------------------
Γ ⊢ f e : N
Dependent functional type | Π(x:M).N
type of return value varies with its argument
Γ, x : M ⊢ b : N Γ ⊢ M : type
--------------------------------
Γ ⊢ λ(x).b : Π(x:M).N
Γ ⊢ f : Π(_:M).N Γ ⊢ e : M
-----------------------------
Γ ⊢ f e : N
Dependent functional type | Π(x:M).N
type of return value varies with its argument
Γ, x : M ⊢ b : N Γ ⊢ M : type
--------------------------------
Γ ⊢ λ(x).b : Π(x:M).N
Γ ⊢ f : Π(x:M).N Γ ⊢ e : M
-----------------------------
Γ ⊢ f e : N
Dependent functional type | Π(x:M).N
type of return value varies with its argument
Γ, x : M ⊢ b : N Γ ⊢ M : type
--------------------------------
Γ ⊢ λ(x).b : Π(x:M).N
Γ ⊢ f : Π(x:M).N Γ ⊢ e : M
-----------------------------
Γ ⊢ f e : N[x:=e]
Dependent functional type | Π(x:M).N
type of return value varies with its argument
Γ, x : M ⊢ b : N Γ ⊢ M : type
--------------------------------
Γ ⊢ λ(x).b : Π(x:M).N
Γ ⊢ f : Π(x:M).N Γ ⊢ e : M
-----------------------------
Γ ⊢ f e : N[x:=e]
Γ ⊢ M : ? Γ, x : M ⊢ N : ?
-----------------------------------
Γ ⊢ Π(x:M).N : ?
Dependent functional type | Π(x:M).N
type of return value varies with its argument
Γ, x : M ⊢ b : N Γ ⊢ M : type
--------------------------------
Γ ⊢ λ(x).b : Π(x:M).N
Γ ⊢ f : Π(x:M).N Γ ⊢ e : M
-----------------------------
Γ ⊢ f e : N[x:=e]
Γ ⊢ M : type Γ, x : M ⊢ N : type
-----------------------------------
Γ ⊢ Π(x:M).N : type
Dependent functional type: simple example
-- A → B ≡ Π(_:A).B
sig id_t : ?
val id_t = λ(X).X → X
Dependent functional type: simple example
-- A → B ≡ Π(_:A).B
sig id_t : type → type
val id_t = λ(X).X → X
Dependent functional type: simple example
-- A → B ≡ Π(_:A).B
sig id_t : type → type
val id_t = λ(X).X → X
sig combine : Π(A:type).A → A → A
Dependent functional type: simple example
-- A → B ≡ Π(_:A).B
sig id_t : type → type
val id_t = λ(X).X → X
sig combine : Π(A:type).A → A → A
sig incr : int → int
val incr = combine int 1
Dependent functional type: simple example
-- A → B ≡ Π(_:A).B
sig id_t : type → type
val id_t = λ(X).X → X
sig combine : Π(A:type).A → A → A
sig incr : id_t int
val incr = combine int 1
Dependent functional type: intuitive example
-- A → B ≡ Π(_:A).B
sig select : int → type
-- with select 0 = string and
-- select i = char for i != 0
Dependent functional type: intuitive example
-- A → B ≡ Π(_:A).B
sig select : int → type
-- with select 0 = string and
-- select i = char for i != 0
sig aString : string
val aString = "Hello World 👋"
sig aChar : char
val aChar = '😀'
Dependent functional type: intuitive example
-- A → B ≡ Π(_:A).B
sig select : int → type
-- with select 0 = string and
-- select i = char for i != 0
sig aString : select 0
val aString = "Hello World 👋"
sig aChar : select 1
val aChar = '😀'
Pairs
λ3: Language λ2 and dependent pair type
e ::=
...
e , e -- Pair
fst e -- Left projection
snd e -- Right projection
...
e * e -- Pair type
Pair type | M * N
Γ ⊢ a : M Γ ⊢ b : N
----------------------
Γ ⊢ a , b : M * N
Γ ⊢ e : M * N Γ ⊢ e : M * N
-------------- ----------------
Γ ⊢ fst e : M Γ ⊢ snd e : N
λ3: Language λ2 and dependent pair type
e ::=
...
e , e -- Pair
fst e -- Left projection
snd e -- Right projection
...
e * e -- Pair type
λ3: Language λ2 and dependent pair type
e ::=
...
e , e -- Pair
fst e -- Left projection
snd e -- Right projection
...
e * e -- ≡ Σ(_:e).e
Σ(x:e).e -- Dependent pair type
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N
-------------------------------------------
Γ ⊢ a , b : M * N
Γ ⊢ p : M * N Γ ⊢ p : M * N
------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N
-------------------------------------------
Γ ⊢ a , b : Σ(_:M).N
Γ ⊢ p : Σ(_:M).N Γ ⊢ p : Σ(_:M).N
----------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N
-------------------------------------------
Γ ⊢ a , b : Σ(x:M).N
Γ ⊢ p : Σ(_:M).N Γ ⊢ p : Σ(_:M).N
----------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N Γ ⊢ M : type
-------------------------------------------
Γ ⊢ a , b : Σ(x:M).N
Γ ⊢ p : Σ(_:M).N Γ ⊢ p : Σ(_:M).N
----------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N[x:=a] Γ ⊢ M : type
-------------------------------------------
Γ ⊢ a , b : Σ(x:M).N
Γ ⊢ p : Σ(_:M).N Γ ⊢ p : Σ(_:M).N
----------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N[x:=a] Γ ⊢ M : type
-------------------------------------------
Γ ⊢ a , b : Σ(x:M).N
Γ ⊢ p : Σ(x:M).N Γ ⊢ p : Σ(_:M).N
----------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N[x:=a] Γ ⊢ M : type
-------------------------------------------
Γ ⊢ a , b : Σ(x:M).N
Γ ⊢ p : Σ(x:M).N Γ ⊢ p : Σ(x:M).N
----------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N[x:=a] Γ ⊢ M : type
-------------------------------------------
Γ ⊢ a , b : Σ(x:M).N
Γ ⊢ p : Σ(x:M).N Γ ⊢ p : Σ(x:M).N
----------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N[x:=fst p]
Dependent pair type | Σ(x:M).N
type of right value varies with its left value
Γ ⊢ a : M Γ ⊢ b : N[x:=a] Γ ⊢ M : type
-------------------------------------------
Γ ⊢ a , b : Σ(x:M).N
Γ ⊢ p : Σ(x:M).N Γ ⊢ p : Σ(x:M).N
----------------- -----------------------
Γ ⊢ fst p : M Γ ⊢ snd p : N[x:=fst p]
Γ ⊢ M : type Γ, x : M ⊢ N : type
-----------------------------------
Γ ⊢ Σ(x:M).N : type
Dependent pair type: simple example
sig pair : ?
val pair = char , '🐶'
Dependent pair type: simple example
sig pair : type * char
val pair = char , '🐶'
Dependent pair type: simple example
sig pair : Σ(x:type).char
val pair = char , '🐶'
Dependent pair type: simple example
sig pair : Σ(x:type).x
val pair = char , '🐶'
Dependent pair type: simple example
sig pair : Σ(x:type).x
val pair = char , '🐶'
sig first : type
val first = fst pair
Dependent pair type: simple example
sig pair : Σ(x:type).x
val pair = char , '🐶'
sig first : type
val first = fst pair
sig second : ?
val second = snd pair
Dependent pair type: simple example
sig pair : Σ(x:type).x
val pair = char , '🐶'
sig first : type
val first = fst pair
sig second : char
val second = snd pair
Dependent pair type: simple example
sig pair : Σ(x:type).x
val pair = char , '🐶'
sig first : type
val first = fst pair
sig second : char -- char ≡ fst pair (i.e. x[x:=fst pair])
val second = snd pair
Dependent pair type: simple example
sig pair : Σ(x:type).x
val pair = (char , '🐶')
sig first : type
val first = fst pair
sig second : fst pair
val second = snd pair
Sum
λ4: Language λ3 and sum type
x ∈ Variables
e ::=
...
inl e -- Left injection
inr e -- Right injection
case x e e -- Catamorphism
...
e + e -- Sum type
Sum type
Γ ⊢ a : ? Γ ⊢ a : ?
------------------ ------------------
Γ ⊢ inl a : ? Γ ⊢ inr a : ?
Γ ⊢ a : ?
Γ ⊢ l : ? Γ ⊢ r : ?
--------------------------------------------------------
Γ ⊢ case a l r : P
Sum type
Γ ⊢ a : M Γ ⊢ a : ?
------------------ ------------------
Γ ⊢ inl a : M + N Γ ⊢ inr a : ?
Γ ⊢ a : ?
Γ ⊢ l : ? Γ ⊢ r : ?
--------------------------------------------------------
Γ ⊢ case a l r : P
Sum type
Γ ⊢ a : M Γ ⊢ a : N
------------------ ------------------
Γ ⊢ inl a : M + N Γ ⊢ inr a : M + N
Γ ⊢ a : ?
Γ ⊢ l : ? Γ ⊢ r : ?
--------------------------------------------------------
Γ ⊢ case a l r : P
Sum type
Γ ⊢ a : M Γ ⊢ a : N
------------------ ------------------
Γ ⊢ inl a : M + N Γ ⊢ inr a : M + N
Γ ⊢ a : M + N
Γ ⊢ l : Π(x:M).P Γ ⊢ r : Π(x:N).P
--------------------------------------------------------
Γ ⊢ case a l r : P
Sum type
Γ ⊢ a : M Γ ⊢ a : N
------------------ ------------------
Γ ⊢ inl a : M + N Γ ⊢ inr a : M + N
Γ ⊢ a : M + N
Γ ⊢ l : Π(x:M).P[a:=inl x] Γ ⊢ r : Π(x:N).P[a:=inr x]
--------------------------------------------------------
Γ ⊢ case a l r : P
Sum type
Γ ⊢ a : M Γ ⊢ a : N
------------------ ------------------
Γ ⊢ inl a : M + N Γ ⊢ inr a : M + N
Γ ⊢ a : M + N
Γ ⊢ l : Π(x:M).P[a:=inl x] Γ ⊢ r : Π(x:N).P[a:=inr x]
--------------------------------------------------------
Γ ⊢ case a l r : P
Γ ⊢ M : type Γ ⊢ N : type
-----------------------------
Γ ⊢ M + N : type
Sum type: simple example
sig int_or_char : int + char → type
val int_or_char = λ(x).case x λ(_).char λ(_).int
sig aChar : char
val aChar = '🌊'
Sum type: simple example
sig int_or_char : int + char → type
val int_or_char = λ(x).case x λ(_).char λ(_).int
sig aChar : int_or_char (inl 1)
val aChar = '🌊'
Sum type: advanced example
sig bool : type
val bool = Unit + Unit
Sum type: advanced example
sig bool : type
val bool = Unit + Unit
sig true : bool
val true = inl unit
sig false : bool
val false = inr unit
Sum type: advanced example
sig bool : type
val bool = Unit + Unit
sig true : bool
val true = inl unit
sig false : bool
val false = inr unit
sig Test : bool → type
val Test = λ(b).case b λ(_).int λ(_).char
Sum type: advanced example
sig bool : type
val bool = Unit + Unit
sig true : bool
val true = inl unit
sig false : bool
val false = inr unit
sig Test : bool → type
val Test = λ(b).case b λ(_).int λ(_).char
sig test : Π(b:bool).?
val test = λ(c).case c λ(_).1 λ(c).'🫣'
Sum type: advanced example
sig bool : type
val bool = Unit + Unit
sig true : bool
val true = inl unit
sig false : bool
val false = inr unit
sig Test : bool → type
val Test = λ(b).case b λ(_).int λ(_).char
sig test : Π(b:bool).(Test b)
val test = λ(c).case c λ(_).1 λ(c).'🫣'
Propositional Equality
- Intentional type theory
- Observational type theory
- Extensional type theory
- Homotopy type theory
λ5: Language λ4 and propositional equality
Intentional type theory
e ::=
...
refl -- Reflexivity
...
e = e -- type equality
λ5: Language λ4 and propositional equality
Intentional type theory
e ::=
...
refl -- Reflexivity
subst e by e -- Substitution
...
e = e -- type equality
Propositional equality
Γ ⊢ n : A Γ ⊢ m : A
-----------------------
Γ ⊢ n = m : type
Propositional equality
Γ ⊢ n : A Γ ⊢ m : A
----------------------- -----------------
Γ ⊢ n = m : type Γ ⊢ refl : m = m
Propositional equality
Γ ⊢ n : A Γ ⊢ m : A
----------------------- -----------------
Γ ⊢ n = m : type Γ ⊢ refl : m = m
Γ ⊢ b : x = B Γ ⊢ a : A[x:=B]
---------------------------------
Γ ⊢ subst a by b : A
Γ ⊢ b : B = x Γ ⊢ a : A[x:=B]
---------------------------------
Γ ⊢ subst a by b : A
Propositional equality: simple example
sig reflexive : Π(A:type).Π(a:A).(a = a)
val reflexive = λ(_).λ(a).refl
Propositional equality: simple example
sig reflexive : Π(A:type).Π(a:A).(a = a)
val reflexive = λ(_).λ(a).refl
sig symmetric : Π(A:type).Π(a:A).Π(b:A).(a = b → b = a)
val symmetric = λ(_).λ(a).λ(b).λ(a=b).?
Propositional equality: simple example
sig reflexive : Π(A:type).Π(a:A).(a = a)
val reflexive = λ(_).λ(a).refl
sig symmetric : Π(A:type).Π(a:A).Π(b:A).(a = b → b = a)
val symmetric = λ(_).λ(a).λ(b).λ(a=b).(subst refl by a=b)
Propositional equality: encoding GADT
-{
data Expr A =
| Boolean of bool with A = bool
| Integer of int with A = int
}-
sig Expr : type → type
val Expr = ?
Propositional equality: encoding GADT
-{
data Expr A =
| Boolean of bool with A = bool
| Integer of int with A = int
}-
sig Expr : type → type
val Expr = λ(A).((A = bool) * bool) + ((A = int) * int)
Propositional equality: encoding GADT
sig Expr : type → type
val Expr = λ(A).((A = bool) * bool) + ((A = int) * int)
Propositional equality: encoding GADT
sig Expr : type → type
val Expr = λ(A).((A = bool) * bool) + ((A = int) * int)
sig Boolean : Π(A:type).Π(_:A = bool).(bool -> Expr A)
val Boolean = λ(_).λ(p).λ(b).inl (p,b)
Propositional equality: encoding GADT
sig Expr : type → type
val Expr = λ(A).((A = bool) * bool) + ((A = int) * int)
sig Boolean : Π(A:type).Π(_:A = bool).(bool -> Expr A)
val Boolean = λ(_).λ(p).λ(b).inl (p,b)
sig Integer : Π(A:type).Π(_:A = int).(int -> Expr A)
val Integer = λ(_).λ(p).λ(i).inr (p,i)
Propositional equality: encoding GADT
sig Expr : type → type
val Expr = λ(A).((A = bool) * bool) + ((A = int) * int)
sig Boolean : Π(A:type).Π(_:A = bool).(bool -> Expr A)
val Boolean = λ(_).λ(p).λ(b).inl (p,b)
sig Integer : Π(A:type).Π(_:A = int).(int -> Expr A)
val Integer = λ(_).λ(p).λ(i).inr (p,i)
sig one_expr : Expr int
val one_expr : Integer int refl 1
Not covered in this presentation
- Implicits and simple type synthesis
- Dependent recursive type
- Dependent record type (Σ type generalisation)
- Russell's Paradox
Conclusion
Think different!
Languages with dependent types
- Coq
- Agda
- Idris
- Lean
- F*
- Granule
- ...